GEOMETRÍA

13 – MAYO – 2020 -- SEMANA 8

OBJETIVOS:

·         Identifica regularidades y argumenta propiedades de figuras geométricas y las aplica en situaciones reales.

·         Resuelve problemas utilizando teoremas básicos

RAZONAMIENTO DEDUCTIVO

El razonamiento entrega argumentos sobre las conexiones mentales incurridas que justifican un determinado pensamiento.

El método deductivo es una estrategia de razonamiento empleada para deducir conclusiones lógicas a partir de una serie de premisas o principios.

RAZONAMIENTO DEDUCTIVO:

El razonamiento deductivo parte de categorías generales para hacer afirmaciones sobre cosas particulares. Va de lo general a lo particular. Es una forma de razonamiento donde se infiere una conclusión a partir de una o varias premisas.

Ejemplos:

Premisa mayor: las galletas tardan 45 minutos en hornearse.

Premisa menor: son las 3:00 pm y Marta mete las galletas al horno.

Conclusión: las galletas estarán listas a las 3:45 pm.

Premisa mayor: todos los martes juan sales 10 minutos antes de su trabajo.

Premisa menor: hoy es martes.

Conclusión: hoy juan saldrá 10 minutos antes de su trabajo.

Premisa mayor: los seres humanos tienen dos manos y dos pies.

Premisa menor: John es un ser humano.

Conclusión: John tiene dos manos y dos pies. 

El razonamiento deductivo: empleado en geometría, consiste en a partir de conocimientos que suponen verdaderos y encadenarlos de tal manera, que se obtengan nuevos conocimientos. Así se demuestran nuevas proposiciones como consecuencia lógica de otras.

Los conocimientos más simples, de los cuales se parte el razonamiento deductivo son las definiciones y los axiomas o postulados. 

Las definiciones: Es una proposición que trata de exponer con claridad y exactitud las características específicas y diferenciadoras de algo material o inmaterial.

  

Los axiomas o postulados: principio fundamental que no puede demostrarse, pero se utiliza para le desarrollo de una teoría. 

Ejemplo: Por dos puntos pasa una única recta.

Ejemplo:   Por un punto pasan infinitas rectas.

En la geometría, existen 5 postulados, expuestos por Euclides.

Euclides (fue un matemático y geómetra griego (ca. 325 a. C.-ca. 265 a. C.). Se le conoce como "el padre de la geometría".

Su obra Elementos es una de las producciones científicas más conocidas del mundo y era una recopilación del conocimiento impartido en el ámbito académico de entonces. En ella se presenta de manera formal, partiendo únicamente de cinco postulados, el estudio de las propiedades de líneas y planos, círculos y esferas, triángulos y conos, etc.; Los teoremas de Euclides son los que generalmente se aprenden en la escuela moderna. Por citar algunos de los más conocidos:

·         La suma de los ángulos interiores de cualquier triángulo es 180°.

·         En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, que es el famoso teorema de Pitágoras.

Los postulados que considero Euclides para la geometría fueron:

11.     Por cualquier parte del punto se puede trazar un segmento de recta.

2.     Todo segmento puede prolongarse indefinidamente.

3.     Dado cualquier segmento, se puede trazar un círculo que tenga el segmento como radio y a uno de sus extremos como centro.

4.     Todos los ángulos rectos son congruentes.

5.     Por un punto exterior a una recta se puede trazar solo una paralela a dicha recta.

Los teoremas son proposiciones lógicas que pueden ser demostradas. Constan de sus hipotesis (lo que se supone) y una tesis (lo que se pretende mostrar).

Importante:

ACTIVIDAD 1

Importante:

ACTIVIDAD 2

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la transcripción de la información y  la  actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: VIERNES  15 DE MAYO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias. 

-------------------------------------------------------------------------------------------------------------------------

22 – ABRIL – 2020 -- SEMANA 7

OBJETIVOS:

·         Identifica regularidades y argumenta propiedades de figuras geométricas y las aplica en situaciones reales.

·         Discrimina casos de semejanza de triángulos en situaciones diversas.

LÍNEAS Y PUNTOS NOTABLES EN UN TRIANGULO

La mediatriz de un segmento es una recta perpendicular que pasa por su punto medio. El punto de corte entre las mediatrices de un triángulo se llama circuncentro. En otras palabras, son, las rectas que pasan por el punto medio de cada uno de sus lados y son perpendiculares a los mismos.

PUNTOS NOTABLES EN UN TRIANGULO:

Circuncentro: es el punto en el que se encuentran las medidas. Este punto no siempre es interior al triangulo, (en los triángulos con un ángulo obtuso, es exterior; en el caso de los triángulos rectángulos, pertenece a la hipotenusa).

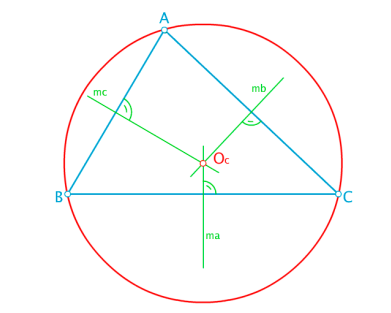
Incentro: es el punto en el que se encuentran las bisectrices. El incentro es siempre interior al triangulo, de ahí su nombre. 

Ortocentro: es el punto de encuentro de las alturas. Este punto no siempre es interior al triangulo

 ACTIVIDAD

observa la información anterior y el siguiente vídeo y responde: 

1.       ¿Qué es mediatriz?

2.       Realiza un ejemplo siguiendo el paso a paso del concepto de mediatriz y explícalo con tus palabras.

3.       ¿Qué es mediatriz de un triángulo?

4.       Realiza un ejemplo siguiendo el paso a paso del concepto de mediatriz de un ángulo y explícalo con tus palabras.

5.       ¿Qué es perpendicular?

6.       ¿Qué es equidistante?

7.       Realiza un mapa conceptual, explicando los puntos notables en un triángulo, y crea un ejemplo para cada uno.

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la transcripción de la información y  la  actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: VIERNES  8 DE MAYO DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias. 

--------------------------------------------------------------------------------------------------------------------------
22 – ABRIL – 2020 -- SEMANA 6

OBJETIVOS:

·         discrimina casos de semejanza de triángulos en situaciones diversas.

·         resuelve problemas que implican aplicación de los criterios de semejanza.

·         compara figuras y argumenta la posibilidad de ser congruente o semejantes entre sí.

SEMEJANZA DE TRIÁNGULOS 

Para dibujar una figura que conserve las proporciones de sus medidas, se emplea una técnica que consiste en trasportar los tamaños aparentes de los objetos con ayuda de un lápiz. Para ello se consiguen los pasos:

1.       Se mira el objeto con un solo ojo, poniendo el lápiz entre el objeto  y el observador  a una determinada distancia y tomando en él la medida del objeto.

2.       Se pone el lápiz con la medida marcada, mirando hacia la superficie donde se desea pintar y acercando el lápiz a una determinada distancia

3.       Se marca la distancia observada sobre la superficie  y se continúa transportado las demás medidas del objeto.

Los triángulos ABC y A’B’C’  tiene la misma forma, aunque su tamaño es distinto: son triángulos semejantes. Esto se puede expresar  también de la siguiente forma:

Dos triángulos son semejantes si podemos transformar  uno en el otro a través de un movimiento     de homotecia (una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor)

ACTIVIDAD

En las ilustraciones siguientes aparecen parejas de figuras  de triángulos que son semejantes  y otras que no lo son, señala la respuesta correcta.

Una característica de los triángulos semejantes es que conservan la medida de sus ángulos correspondientes, y además mantienen la razón entre sus lados. Por ejemplo, en los siguientes triángulos semejantes ABC y A’B’C’ podemos escribir estas congruencias:

Angulo A es congruente con A’ y se simboliza así: ∢A = ∢A’

Angulo B es congruente con B’ y se simboliza así: ∢B = ∢B’

Angulo C es congruente con C’ y se simboliza así: ∢C = ∢C’

Si dos triángulos son semejantes, entonces sus ángulos correspondientes son congruentes y la razón entre sus lados correspondientes se conserva.

CASOS DE SEMEJANZA DE TRIÁNGULOS:

Veremos que cuando deseamos determinar la semejanza de dos triángulos, es suficiente con  tres condiciones.

CRITERIO ÁNGULO  -  ÁNGULO: Andrés y Natalia están jugando con sombras. Tiene una serie de triángulos recortados en una cartulina y con una linterna proyectan su sombra  contra la pared. Natalia tiene un triangulo cuyos ángulos mas grandes miden 60° y 70°, respectivamente, y su sombra en la pared es un triángulo cuyos ángulos mas grandes también miden 60° y 70°. Andrés marca los vértices sobre el triángulo de la pared y recordando que los ángulos interiores de un triángulo suman 180°, deduce que el ángulo mas pequeño debe medir 50°.

Dos triángulos son semejantes si por lo menos dos de sus ángulos  son congruentes. Este es el criterio ángulo – ángulo.

CRITERIOS PROPORCIÓN ENTRE LOS LADOS:

Los dos amigos continúan proyectando sombras. Ahora Natalia tiene un triangulo cuyos lados miden 5cm, 7cm, y 9cm. Lo ilumina hasta obtener una sombra en la que los lados miden 40 cm, 56 cm y 72 cm, respectivamente. Andrés le dice que los triángulos los semejantes porque al dividir  los lados correspondientes da como resultado 8:

40÷5,  56÷7,  72÷9

Dos triángulos son semejantes si conservan la razón entre sus lados correspondientes, es decir, si sus lados son proporcionales. Este es el criterio proporción entre todos sus lados. 

CRITERIO PROPORCIÓN DE SUS LADOS Y CONGRUENCIA DEL ÁNGULO ENTRE ELLOS:

Por último Natalia tiene dos triángulos recortados en cartulina. Para comprobar que son semejantes, Andrés pega el más grande en la pared y con la linterna proyecta el pequeño hasta que la sombra del uno coincide con el tamaño del otro.

Andrés observa que entre las medidas de los lados se cumple que:

12÷3, 8÷3

Dos triángulos son semejantes si conservan la razón entre dos de sus lados correspondientes y el ángulo entre ellos es congruente.

                                                                    

                                          

ACTIVIDAD

1.       observa la imagen y analiza si los dos triángulos son semejantes e indica el criterio utilizado 

1.       establece si las siguientes parejas de triángulos son semejantes y explica en cada caso  el criterio utilizado.

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la transcripción de la información y  la  actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: VIERNES  1 DE MAYO  DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias. 

--------------------------------------------------------------------------------------------------------------------------
22 – ABRIL – 2020 -- SEMANA 5

OBJETIVOS:

·         IDENTIFICA RELACIONES DE CONGRUENCIA Y SEMEJANZA ENTRE LAS FORMAS GEOMÉTRICAS QUE CONFIGURAN EL DISEÑO DE UN OBJETO.

·         UTILIZA CRITERIOS PARA ARGUMENTAR LA CONGRUENCIA DE DOS TRIÁNGULOS.

·         DISCRIMINA CASOS DE SEMEJANZA DE TRIÁNGULOS EN SITUACIONES DIVERSAS.

·         RESUELVE PROBLEMAS QUE IMPLICAN APLICACIÓN DE LOS CRITERIOS DE SEMEJANZA.

NOTACIÓN DE LA RELACIÓN DE CONGRUENCIA ENTRE TRIÁNGULOS

Los triángulos ABC y XYZ son congruentes. Las marcas iguales sobre los triángulos indican cuáles ángulos y lados son congruentes. Para indicar esta congruencia, podemos escribir ABC > XYZ. El siguiente diagrama muestra como esta notación proporciona información específica sobre las partes (ángulos y lados) que se corresponden.

Observa que no sería correcto simbolizar esta congruencia entre los triángulos de otra forma. Por ejemplo, si escribiremos:

ΔABC ≅ ΔXZY y estaríamos afirmando que el segmento AB congruente con XZ lo cual no necesariamente es cierto.

EJEMPLO : 

La congruencia de triángulos es muy útil para verificar o demostrar relaciones entre diferentes figuras o entre elementos de figuras. En la imagen se muestra un rectángulo ABCD con sus dos diagonales AC y BD.

Gracias la congruencia de triángulos y específicamente a los criterios de congruencia podemos afirmar que dichas diagonales son iguales. Veamos:

Por definición de rectángulo, los lados AB y CD son congruentes al igual que los lados AD y BC. Además, tenemos que ∡ABC ≅ ∡ADC ya que ambos son ángulos restos. Entonces por el criterio de congruencia LAL podemos afirmar que los triángulos ABC Y CDA son congruentes (ΔABC ≅ CDA).

Esto significa que las demás partes correspondientes son también congruentes. Es decir, también es cierto que las diagonales AC y BD son congruentes. 

EJEMPLO:

ACTIVIDAD

1.   En las siguientes parejas de triángulos se conocen las congruencias que se indican.  Responde las preguntas que aparecen en cada caso.

a.    Lado AB = lado DF; lado BC = lado FE; ∢ B = ∢ F

¿Qué ángulo es congruentes con A?

¿Qué ángulo es congruente con C?

a.    ∢ A = ∢ F; lado AC = lado FE; ∢ B = ∢ D

¿Qué ángulo es congruente con E?

¿Qué lado es congruente con B?

a.    Lado AC = lado DF; lado AB = lado DE; lado BC = lado EF

¿Qué ángulo es congruente con B?

¿Qué ángulo es congruente con A?

1.   Supón que se tiene dos triángulos ΔTUV y ΔMPN con las siguientes relaciones entre sus partes:

∢ T ≅ ∢ M

∢ U ≅ ∢ P

∢ V ≅ ∢ N

TU = PM

TV = NM

UV = PN

Completa correctamente la afirmación sobre la congruencia de triángulos:

Δ _ _ _  ≅   Δ _ _ _

1.   Si ΔACD ≅ ΔMBN, ¿Cuál es el lado congruente de lado AD? ¿Cuál es el ángulo congruente ∢ ADC?

2.   ¿De que otra manera se puede simbolizar ΔABC ≅ ΔXYZ?

3.   Si ΔXYZ es un triángulo equilátero, el cual es congruente a ΔPQR, escribe todas las formas posibles de simbolizar esta relación.

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la transcripción de la información y  la  actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: LUNES  27  DE ABRIL  DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias. 

--------------------------------------------------------------------------------------------------------------------------

15 – ABRIL – 2020  -- SEMANA 4

OBJETIVOS:

• Identifica relaciones de congruencia y semejanza entre las formas geométricas que configuran el diseño de un objeto.

• Utiliza criterios para argumentar la congruencia de dos triángulos.

• Compara figuras y argumenta la posibilidad de ser congruente o semejantes entre sí.

CASOS DE CONGRUENCIAS DE TRIÁNGULOS

Ya sabemos que dos triángulos son congruentes si tienen sus seis elementos correspondientes congruentes, sus tres lados y sus tres ángulos. Así, cuando se requiere determinar la congruencia de dos triángulos no es necesario verificar la correspondencia entre los seis elementos, es suficiente con tres elementos. 

CRITERIO LADO – LADO – LADO (LLL):

Natalia y Andrés juegan a dibujar triángulos congruentes. Después de hacer el primero sin que Andrés vea su trabajo, Natalia le dice que haga uno cuyos lados midas: 3 cm, 4 cm, y 6 cm, respectivamente. Natalia quiere ver si Andrés construye un triángulo distinto del que ella dibujó. Hecho el trabajo, lo comparan y encuentran los dibujos.

Para verificar que los dos triángulos elaborados son congruentes, deciden recortarlos y ponerlos uno encima del otro. De esta manera se dan cuenta de que los elementos que componen las dos figuras coinciden. De allí concluyen:

Dos triángulos son congruentes cuando los tres lados de uno de ellos son congruentes con los tres lados respectivos del otro. Este es el criterio de lado – lado – lado, que en forma abreviada se escribe LLL.  

CRITERIO LADO – ÀNGULO – LADO (LAL):

Natalia y Andrés continúan jugando, solo que esta vez es él quien hace primero un triángulo, y luego le dice a ella que dibuje uno con dos lados que midan 10 y 15 cm, con un dato adicional: el ángulo que forma estos lados debe medir 60º. Con esta información, ella procura elaborar dos triángulos distintos.

Para verificar que tales triángulos son congruentes, los recortan y los superponen. Esto les permiten observar si dos de los lados y el ángulo que forman coinciden o no. En este caso coinciden; luego se congruentes que los triángulos son congruentes.

Dos triángulos son congruentes cuando tienen, respectivamente, congruentes dos lados y el ángulo que forma dichos lados.

Este es el criterio lado – ángulo – lado, abreviado como LAL.

CRITERIO ÀNGULO – LADO – ÀNGULO:

Por último, los dos amigos dibujan, cada uno por separado dos triángulos que tienen ángulos de 4º y 120º, y el lado entre dichos ángulos mide 4 cm. Cuando comparan los triángulos dibujados se encuentran con:

Para verificar que tales triángulos son congruentes, los recortan y los superponen. Llegan a la conclusión de que con las tres condiciones dadas siempre obtendrán un triángulo congruente.

Dos triángulos son congruentes cuando tienen, respectivamente, congruentes dos ángulos y el lado que se encuentra entre ellos.

Este es el criterio ángulo – lado- ángulo, que se abrevia ALA.

ACTIVIDAD

1.       observa las siguientes parejas de triángulos congruentes. Indica en cada caso què pareja de ángulos y de lados son congruentes. 

1.       en las siguientes parejas de triángulos, las marcas semejantes indican los lados o los ángulos congruentes. Indica para cada caso, si existe, cuál de los tres criterios de congruencia (LLL, LAL, ALA) demostraría esta condición.  

1.       responde:

realiza un ejemplo, para explicar el concepto de congruencia

• ¿Qué es el criterio de lado – lado – lado? - ejemplo
• ¿Qué es el criterio de lado – ángulo – lado? - ejemplo
• ¿Qué es el criterio de ángulo – lado – ángulo? – ejemplo
• Menciona las diferencias de estos tres criterios

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la transcripción de la información y  la  actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: VIERNES  17  DE ABRIL  DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias. 

--------------------------------------------------------------------------------------------------------------------------
01 – ABRIL - 2020-

TRIÁNGULOS

Un triángulo es el polígono que resulta de unir 3 puntos con líneas rectas. Todo triángulo tiene 3 lados (a, b y c), 3 vértices (A, B y C) y 3 ángulos interiores (a, b y g).

Los triángulos podemos clasificar los según 2 criterios:

Según la medida de sus lados

- Equilátero: los 3 lados son iguales  

- Isósceles: tienen 2 lados iguales y un lado distinto

Escaleno: los 3 lados son distintos

Según la medida de sus ángulos:

- Acutángulo: los 3 ángulos miden  menos de 90 grados

 Rectángulo: tiene uno de sus lados recto,  (90 grados)

Obtusángulo: el ángulo interior mide (más de 90 grados):

CONGRUENCIA DE TRIÁNGULOS

Don triángulos son congruentes si es posible transformar uno en el otro a través de movimientos.

Dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas.

Observa con atención el siguiente vídeo:   

ACTIVIDAD

Dibuja en tu cuaderno las siguientes figuras. Existen  solo 3 parejas de triángulos congruentes y una que no lo es; escribe debajo de cada imagen si son congruentes, o  no son congruentes.

Con ayuda del vídeo y el texto anterior , responde las siguientes preguntas:

¿Qué significa la palabra congruencia?

¿Qué es un triángulo?

¿Qué es un triángulo isósceles?

¿Qué es un triángulo equilátero?

¿Qué es un triángulo escaleno?

Menciona mínimo tres  características de los siguientes triángulos:

·         Triángulo acutángulos

·         Triángulo  rectángulo

·         Triángulo obtusángulo

¿Los triángulos de la imagen anterior son congruentes? ¿Por qué?

R-

                       

IMPORTANTE TENER EN CUENTA:

1. tomar foto de la transcripción de la información y  la  actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: VIERNES  03 DE ABRIL  DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias. 

------------------------------------------------------------------------------------------------------------

24 - MARZO-2020

POLÍGONOS 

ELEMENTOS DE UN POLÍGONO 
un polígono es una figura plana limitada por segmentos unidos en sus extremos de manera que:

1. en un punto, se unen exactamente dos segmentos.
2. cada segmento esta unido con otros dos segmentos. 

Los polígonos están compuesto por varios segmentos que son llamados lados, y los puntos de encuentros son denominados vértices, cuando estos lados se unen forman un ángulo que será el elemento característico del polígono

en un polígono se identifican los siguientes elementos:



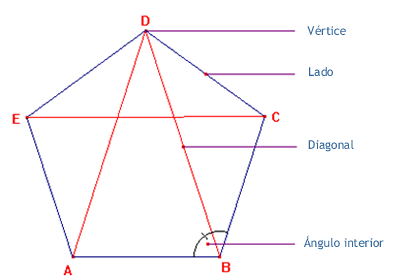
los vértices son los puntos 
A, B, C, D,  y E.

los lados son los segmentos

AB  BC  CD  DE  EA

los ángulos interiores son 

angulo A, angulo B, angulo C, angulo D, angulo E.

las diagonales son los segmentos cuyos extremos son dos vértices no consecutivos del polígono.

ACTIVIDAD

observa la siguiente imagen: 

1. en el polígono  C, D, E, B, A, nombra:

• los vértices
• los ángulos interiores
• los lados 

CLASIFICACIÓN DE LOS POLÍGONOS:

los polígonos se pueden clasificar según: su numero de lados, su forma y la medida de sus lados y sus ángulos

NUMERO DE LADOS. 

según el numero de lados, cada polígono recibe un nombre especial:

3 lados	Triángulo
4 lados	cuadrilátero
5 lados	Pentágono
6 lados	Hexágono
7 lados	Heptágono
8 lados	Octágono
9 lados	Nonágono
10 lados	Decágono
11 lados	Undecágono
12 lados	Dodecágono

ACTIVIDAD

1. llena en tu cuaderno  la siguiente tabla con el ejemplo correspondiente, y señala en cada caso:

• los vértices 
• los lados
• los ángulos interiores 

No  de  lados	Nombre	Ejemplo
3	Triángulo
4	cuadrilátero
5	Pentágono
6	Hexágono
7	Heptágono
8	Octágono
9	Nonágono
10	Decágono
11	Undecágono
12	Dodecágono

MPORTANTE TENER EN CUENTA: 

1. tomar foto de la transcripción de la información, con las imágenes graficadas y  la  actividad desarrollada en el cuaderno, enviarla al correo murilloviviana82@gmail.com. Por favor enviar un solo correo con todas las fotos relacionadas a mis áreas.

2. fecha de entrega de la actividad desarrollada: VIERNES  27  DE MARZO  DEL 2020.

3. especificar: nombres, apellidos, grado del estudiante y materias. 

----------------------------------------------------------------------------------------------------------------------------------

clasificación de ángulo según la suma de sus medidas

De acurdo con la suma  de sus medidas, dos ángulos pueden ser complementarios o suplementarios.

Ángulos complementarios:  la suma de sus medidas es 90°. por ejemplo: 

Si el angulo uno mas el angulo dos es igual a  90°.

Si el angulo uno es el complemento del angulo dos o el angulo dos es el complemento del angulo uno. 

Ángulos suplementarios: la suma de sus medidas es 180° . por ejemplo:

Si el angulo uno mas el angulo dos es igual a 180° se dice que:

El angulo uno es el suplemento del angulo dos o el angulo dos es el suplemento del angulo uno.

clasificación de ángulos según su posición

Según su posición, dos ángulos pueden ser consecutivos, Adyacentes u opuestos por el vértice. 

Ángulos consecutivos: tiene el mismo vértice y uno de sus lados es común.

Ángulos adyacentes: son consecutivos y sus lados no comunes están en la misma recta. 

Ángulo opuestos por el vértice: están formados entre dos rectas que se intersecan en un punto. Dicho punto es el vértice de los ángulos.

A partir de la clasificación anterior se cumplen las siguientes propiedades.

PROPIEDAD 1: dos ángulos adyacentes son suplementarios 

PROPIEDAD 2: dos ángulos opuestos por el vértice tiene la misma amplitud.  

ACTIVIDAD

1. Leer cada enunciado. luego determinar si la afirmación es falsa o verdadera. justifica la respuesta.

------ Un ángulo es complementario de otro si es menor de 90°.

------ Dos ángulos agudos siempre son complementarios.

------ Un ángulo llano es suplementario de un ángulo de 0°.

------ Si un ángulo mide 30°, su complemento es un ángulo que mide el doble.

------ Si un ángulo mide 90°, su suplemento es un ángulo recto.

------ Un ángulo agudo puede ser el suplemento de un ángulo  obtuso.

------ Dos ángulos obtusos no pueden ser suplementarios.

2. completa las afirmaciones con las palabras a veces, siempre o nunca 

---------- los ángulos adyacentes son suplementarios 

---------- Los ángulos suplementarios son adyacentes.

---------- Los ángulos opuestos por el vértice son iguales.

---------- El suplemento de un ángulo recto es un ángulo recto.

---------- El complemento de un ángulo es mayor que el ángulo.

IMPORTANTE TENER EN CUENTA: 

1. tomar foto de la actividad desarrollada en el cuaderno, al correo murilloviviana82@gmail.com

2. fecha de entrega de la actividad desarrollada: MARTES, 24 DE MARZO DEL 2020.

3. nombre completo del estudiante y el grado 

NOTA: todo la explicación anterior debe ir registrada en el cuaderno, por favor enviar a mi correo (murilloviviana82@gmail.com - especificar el nombre, apellido y grado del estudiante ) la solución de los puntos anteriores a través de una fotografía.